4. 语言模型平滑算法

由于训练语料的有限，大量的N-gram词语在训练语料中没有出现，而前文提到N-gram的训练一般采用最大似然估计的方法，这就导致了零概率问题。同时最大似然估计对于小频率词语的估计也很糟糕。这就是语言模型的数据稀疏问题。

为了解决数据稀疏问题，提出了一系列的平滑算法，基本思想是降低已出现N-gram条件概率分布，以使未出现的N-gram条件概率分布非零，且经数据平滑后保证概率和为1。

1. Laplace平滑

Laplace平滑算法也称为Add-one平滑，是最简单的平滑算法。其基本思想是，在每个N-gram的次数上加上1，保证每个N-gram至少出现1次。

Ci是词语的个数，Nall是训练语料中所有词数，V是词典中词语总数。

2 Good-Turing平滑

Good-Turing平滑是通过折扣出现c+1次的所有N-gram的个数到出现c次的N-gram的个数来实现平滑。Nc是所有出现c次的所有N-gram的个数。

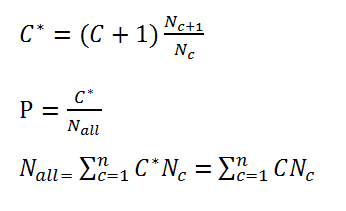
3 Interpolation平滑(插值平滑)

Laplace平滑和Good-Turing平滑算法对于训练语料中没有出现的N-gram都一视同仁，概率相等，这显然不太合理。比如：

假设 C(be happy) = C(be zzz) = 0, 很明显感觉be happy出现的概率应该要比be zzz大一些。

为此提出了线性插值平滑算法，也称为Jelinek-Mercer smoothing，其基本思想是将高阶模型和低阶模型作线性组合，利用低元N-gram模型对高元N-gram模型进行线性插值。因为在没有足够的数据对高元n-gram模型进行概率估计时，低元n-gram模型通常可以提供有用的信息。

对于bigram，其公式如下：

同理对于N-gram:

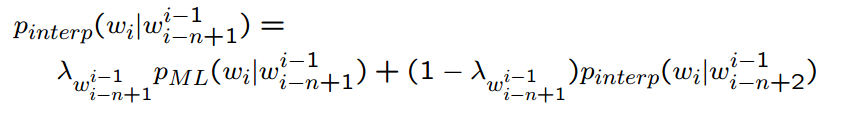
其中λ可以通过EM算法在Held-out数据集上估计学习得到。

4 Katz回退(Back-off)

回退算法的思想是如果高阶的语言模型概率为0，那么回退到低阶，用低阶的概率来计算高阶的概率，是实际最常用的方法，常见的ARPA格式的语言模型，（概率 词语 回退概率），就是采用回退的表示。 Katz回退算法的公式如下：

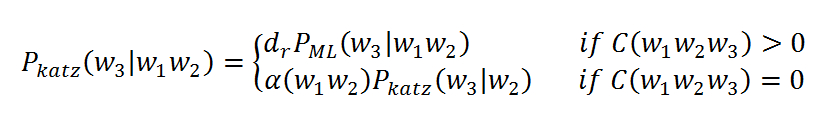
其中dr是折扣因子，即将出现的高阶语言模型的概率打折，是剩下的部分分配给经过的回退的语言模型上，保证总概率为1.dr是经过Good-Turing算法计算得到，

。

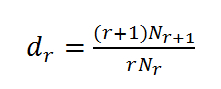α是回退系数，保证最终的概率总和为0。

于是α的值为

参考

有关语言模型的平滑算法， 《An Empirical Study of Smoothing Techniques for Language Modeling》这篇论文介绍的很详细，可以参考。

上一篇 统计语言模型